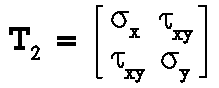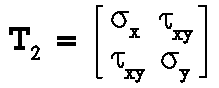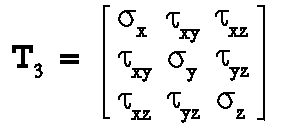Mohr's Circle for 2-D Stress Analysis

If you want to know the principal stresses and maximum shear stresses, you can simply make it through 2-D or 3-D Mohr's cirlcles!

You can know about the theory of Mohr's circles from any text books of Mechanics of Materials. The following two are good references, for examples.

1. Ferdinand P. Beer and E. Russell Johnson, Jr, "Mechanics of Materials", Second Edition, McGraw-Hill, Inc, 1992.
2 . James M. Gere and Stephen P. Timoshenko, "Mechanics of Materials", Third Edition, PWS-KENT Publishing Company, Boston, 1990.

The 2-D stresses, so called plane stress problem, are usually given by the three stress components s_x, s_y, and t_xy , which consist in a two-by-two symmetric matrix (stress tensor):

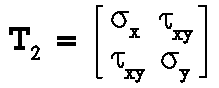
(1)

What people usually are interested in more are the two prinicipal stresses s₁ and s₂ , which are the two eigenvalues of the two-by-two symmetric matrix of Eqn (1), and the maximum shear stress t_max , which can be calculated from s₁ and s₂ . Now, see the Fig. 1 below, which represents that a state of plane stress exists at point O and that it is defined by the stress components s_x, s_y, and t_xy associated with the left element in the Fig. 1. We propose to determine the stress components s_xq, s_yq, and t_xyqassociated with the right element after it has been rotated through an angle q about the z axis.

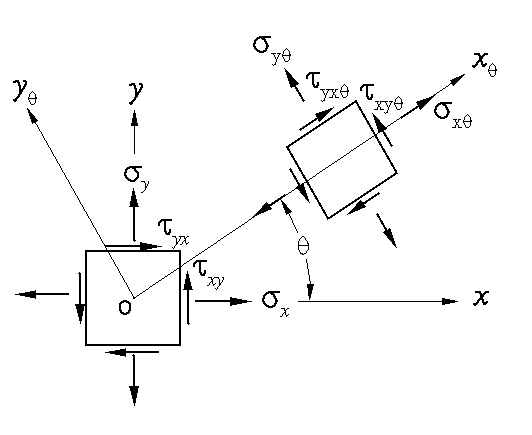Fig. 1 Plane stresses in different orientations

Then, we have the following relationship:

s_xq= s_xcos ²q + s_ysin²q + 2 t_xy sin q cos q

(2)

and t_xyq= -(s_x- s_y) cos²q + t_xy (cos²q - sin²q)

(3)

Equivalently, the above two equations can be rewritten as follows: s_xq= (s_x + s_y)/2 + (s_x - s_y)/2 cos 2q + t_xy sin 2q

(4)

and t_xyq= -(s_x - s_y)/2 sin 2q + t_xy cos 2q

(5)

The expression for the normal stress s_yqmay be obtained by replacing the q in the relation for s_xqin Eqn. 3 by q + 90^o, it turns out to be s_yq= (s_x + s_y)/2 - (s_x - s_y)/2 cos 2q - t_xy sin 2q

(6)

From the relations for s_xqands_yq, one obtains the circle equation: (s_xq- s_ave)²+ t²_xyq_{= R}²_m

(7)

where s_ave= (s_x + s_y)/2 = (s_xq + s_yq)/2 ; _{Rm
= [}(s_x - s_y)²/ 4 + t²_xy_]^1/2

(8)

This circle is with radius _R²_mand centered at C=(s_ave
,0) if let s = s_xqand t = -t_xyqas shown in Fig. 2 below - that is right the Mohr's Circle for plane stress problem or 2-D stress problem!

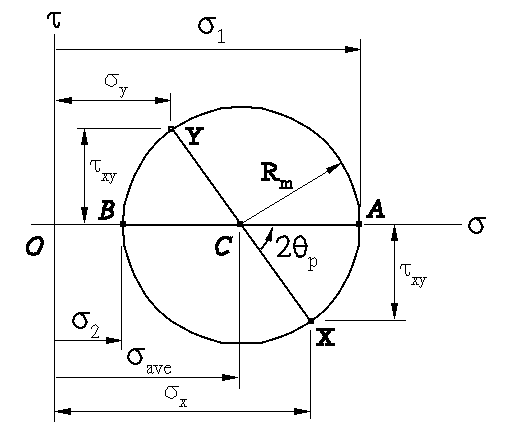Fig. 2 Mohr's circle for plane (2-D) stress In fact, Eqns. 4 and 5 are the parametric equations for the Mohr's circle! In Fig. 2, one reads that the point
X = (s_x , -t_xy )

(9)

which corresponds to the point at which q = 0 and the point A = (s₁ , 0 )

(10)

which corresponds to the point at which q = q_pthat gives the principal stress s₁! Note that tan 2q_p
=2t_xy /(s_x - s_y)

(11)

and the point Y = (s_y , t_xy )

(12)

which corresponds to the point at which q = 90^o and the point B = (s₂ , 0 )

(13)

which corresponds to the point at which q = q_p+90^o that gives the principal stress s₂! To this end, one can pick the maxium normal stressess as s_max
=max(s₁, s₂), s_min
=min(s₁, s₂)

(14)

Besides, finally one can also read the maxium shear stress as t_{max
= Rm =
[}(s_x - s_y)²/ 4 + t²_xy_]^1/2

(15)

which corresponds to the apex of the Mohr's circle at which q = q_p+45^o ! (The end.)

Mohr's Circles for 3-D Stress Analysis

The 3-D stresses, so called spatial stress problem, are usually given by the six stress components s_x , s_y , s_z , t_xy , t_yz , and t_zx , (see Fig. 3) which consist in a three-by-three symmetric matrix (stress tensor):

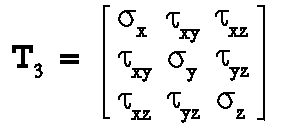
(16)

What people usually are interested in more are the three prinicipal stresses s₁ , s₂ , and s₃ , which are eigenvalues of the three-by-three symmetric matrix of Eqn (16) , and the three maximum shear stresses t_max1 , t_max2 , and t_max3 , which can be calculated from s₁ , s₂ , and s₃ .

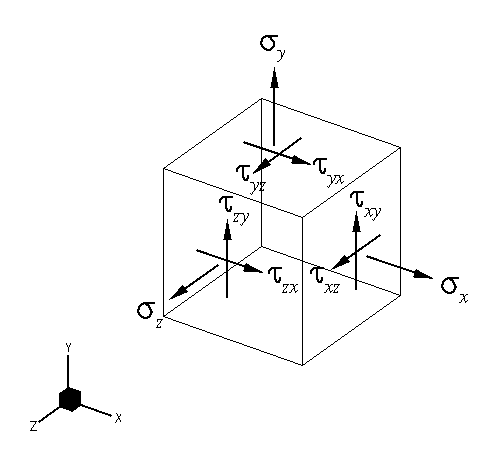Fig. 3 3-D stress state represented by axes parallel to X-Y-Z

Imagine that there is a plane cut through the cube in Fig. 3 , and the unit normal vector n of the cut plane has the direction cosines v_x, v_y, and v_z, that is

n = (v_x , v_y , v_z)

(17)

then the normal stress on this plane can be represented by s_n= s_xv²_x+ s_yv²_y+ s_zv²_z+ 2 t_xyv_xv_y+ 2 t_yzv_yv_z+ 2 t_xzv_xv_z

(18)

There exist three sets of direction cosines, n₁, n₂, and n₃ - the three principal axes, which make s_nachieve extreme values s₁, s₂, and s₃- the three principal stresses, and on the corresponding cut planes, the shear stresses vanish! The problem of finding the principal stresses and their associated axes is equivalent to finding the eigenvalues and eigenvectors of the following problem: (sI₃ - T₃)n = 0

(19)

The three eigenvalues of Eqn (19) are the roots of the following characteristic polynomial equation: det(sI₃ - T₃) = s³ - As² + Bs - C = 0

(20)

where A = s_x+ s_y+ s_z

(21)

B = s_xs_y + s_ys_z + s_xs_z - t²_xy - t²_yz - t²_xz

(22)

C = s_xs_ys_z+ 2 t_xyt_yzt_xz - s_xt²_yz- s_yt²_xz- s_zt²_xy

(23)

In fact, the coefficients A, B, and C in Eqn (20) are invariants as long as the stress state is prescribed(see e.g. Ref. 2) . Therefore, if the three roots of Eqn (20) are s₁, s₂, and s₃,one has the following equations: s₁+ s₂+ s₃= A

(24)

s₁s₂ + s₂s₃ + s₁s₃= B

(25)

s₁s₂s₃= C

(26)

Numerically, one can always find one of the three roots of Eqn (20) , e.g. s₁, using line search algorithm, e.g. bisection algorithm. Then combining Eqns (24)and (25), one obtains a simple quadratic equations and therefore obtains two other roots of Eqn (20), e.g. s₂ and s_3
.To this end, one can re-order the three roots and obtains the three principal stresses, e.g. s₁= max(s_1
, s_2
, s₃)

(27)

s₃= min(s_1
, s_2
, s₃)

(28)

s₂= (A - s₁- s₂)

(29)

Now, substituting s₁, s₂, or s₃into Eqn (19), one can obtains the corresponding principal axes n₁, n₂, or n₃, respectively.

Similar to Fig. 3, one can imagine a cube with their faces normal to n₁, n₂, or n₃. For example, one can do so in Fig. 3 by replacing the axes X,Y, and Z with n₁, n₂, and n₃, respectively, replacing the normal stresses s_x , s_y , and s_z with the principal stresses s₁, s₂, and s₃, respectively, and removing the shear stresses t_xy , t_yz , and t_zx .

Now, pay attention the new cube with axes n₁, n₂, and n₃. Let the cube be rotated about the axis n₃, then the corresponding transformation of stress may be analyzed by means of Mohr's circle as if it were a transformation of plane stress. Indeed, the shear stresses excerted on the faces normal to the n₃axis remain equal to zero, and the normal stress s₃is perpendicular to the plane spanned by n₁and n₂in which the transformation takes place and thus, does not affect this transformation. One may therefore use the circle of diameter AB to determine the normal and shear stresses exerted on the faces of the cube as it is rotated about the n₃axis (see Fig. 4). Similarly, the circles of diameter BC and CA may be used to determine the stresses on the cube as it is rotated about the n₁and n₂ axes, respectively.

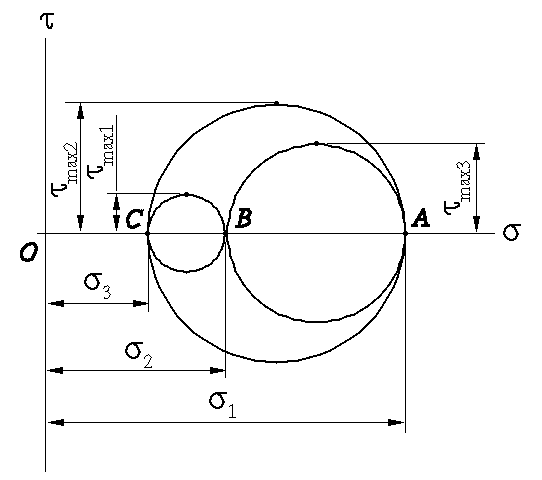Fig. 4 Mohr's circles for space (3-D) stress

What if the rotations are about the axes rather than principal axes? It can be shown that any other transformation of axes would lead to stresses represented in Fig. 4 by a point located within the area which is bounded by the bigest circle with the other two circles removed!

Therefore, one can obtain the maxium/minimum normal and shear stresses from Mohr's circles for 3-D stress as shown in Fig. 4!

Note the notations above (which may be different from other references), one obtains that

s_max= s₁

(30)

s_min= s₃

(31)

t_max= (s₁- s₃)/2 = t_max2

(32)

Note that in Fig. 4, t_max1, t_max2, and t_max3are the maximum shear stresses obtained while the rotation is about n₁, n₂, and n₃, respectively. (The end.)

Mohr's Circles for Strain and for Moments and Products of Inertia

Mohr's circle(s) can be used for strain analysis and for moments and products of inertia and other quantities as long as they can be represented by two-by-two or three-by-three symmetric matrices (tensors). (The end.)